実用上、本当に速いコードを書くにはまず正しいアルゴリズムの選択から。本書は実践的側面を重視した、新しいタイプのアルゴリズム事典です。どのアルゴリズムを使うべきか、どう実装するのか、さらに性能を向上させる方法はあるのかを解説。主要な40余りのアルゴリズムを網羅し、C、C++、Java、Pythonでの実装例を示します。改訂版では、フォーチュンアルゴリズム、マージソート、マルチスレッドクイックソート、AVL平衡二分木、R木と四分木などの新たなアルゴリズムを追加。実際にベンチマークを取る手法も紹介した実際的、実践的な一冊です。 使用サンプルコード、収録データはGitHubから取得可能です。
アルゴリズムクイックリファレンス 第2版
![[cover photo]](https://www.oreilly.co.jp/books/images/picture_large978-4-87311-785-0.jpeg)
- TOPICS
- Programming
- 発行年月日
- 2016年12月
- PRINT LENGTH
- 440
- ISBN
- 978-4-87311-785-0
- 原書
- Algorithms in a Nutshell, 2nd Edition
- FORMAT
- Print PDF
正誤表
ここで紹介する正誤表には、書籍発行後に気づいた誤植や更新された情報を掲載しています。以下のリストに記載の年月は、正誤表を作成し、増刷書籍を印刷した月です。お手持ちの書籍では、すでに修正が施されている場合がありますので、書籍最終ページの奥付でお手持ちの書籍の刷版、刷り年月日をご確認の上、ご利用ください。
第1、2刷正誤表
第1刷、2刷正誤表
2019年1月30日更新
203ページ、1行目の数式
【誤】
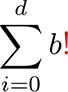
【正】
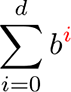
211ページ、アルファベータ法擬似コード12~15行目
【誤】
foreach valid move m for player in state s do execute move m on s [move, score] = alphaBeta (s, ply-1, opponent, player, -high, -low) undo move m on s
【正】
foreach (状態sにおいてplayerが指せる有効な手m) do sで手mを実行する [move, score] = alphaBeta (s, ply-1, opponent, player, -high, -low) sで手mを取り消す
263ページ、12行目*1
[*1] 原書正誤表に従い修正
【誤】
Gm内に容量k(v)の辺(vb, w)を作る。
【正】
Gm内に容量min(k(v), c(v, w))の辺(vb, w)を作る。
265ページ、図8-6の右側の図
【誤】
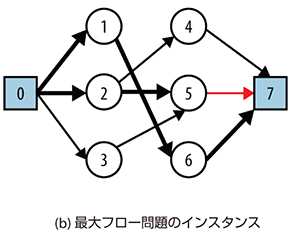
【正】
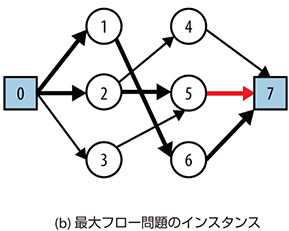
273ページ、14行目*2
[*2] 原書正誤表に従い修正
【誤】
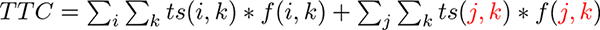
【正】
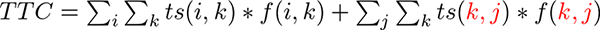
273ページ、下から3行目*3
[*3] 原書正誤表に従い修正
【誤】
需要基地tjは、1+m+2*w+jに対応する
【正】
需要基地tjは、m+2*w+jに対応する
274ページ、図8-8上
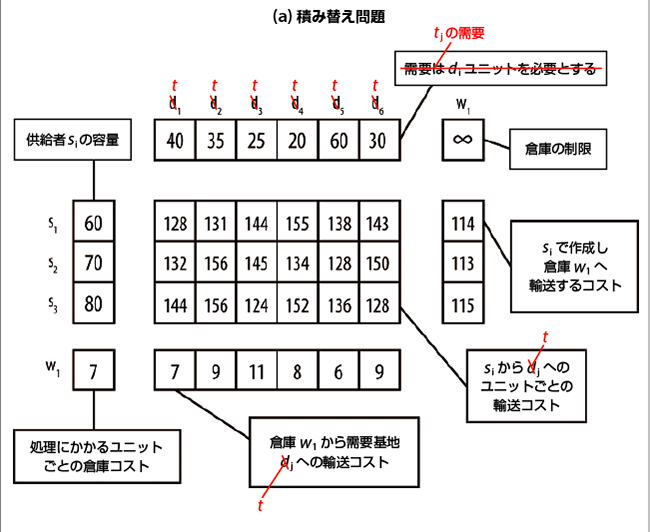
276ページ、下から7行目
【誤】
ソース節点から出る辺の総和は、その供給と等しくなければならない。需要節点へ入る辺の総和は、需要と等しくなければならない。
【正】
ソース節点から出る辺のフローに対応する変数の値の総和は、その供給と等しくなければならない。需要節点へ入る辺のフローに対応する変数の値の総和は、需要と等しくなければならない。
285ページ、図9-2の下の式*4
[*4] 原書正誤表に従い修正
【誤】
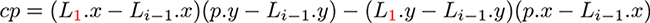
【正】
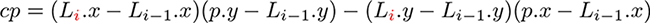
291ページ、下から2行目*5
[*5] 原書正誤表に従い修正
【誤】
平衡二分木を使った実装が、比較を使った整列技法による方式の中では最良の性能を示している。バケツソートを使った実装は最も効率が良いが、これは、入力集合が一様分布から採られたからである。一般には、凸包計算はO(n log n) の性能となる。
【正】
一般には、凸包計算はO(n log n) の性能となる。バケツソートを使った実装は最も効率が良いが、これは、入力集合が一様分布から採られたからである。
314ページ、例9-6、7行目
【誤】
ightA = node.getRightAncestor()
【正】
rightA = node.getRightAncestor()
327ページ、最近傍法の疑似コード下から7行目
【誤】
if node が x より上にある then
【正】
if x が node より上にある then
351ページ、下から1行目
【誤】
もう1つの関連する定数は⌈M/2⌉で、
【正】
もう1つの関連する定数は⌊M/2⌋で、
目次
第2版日本語版へ寄せて
第2版まえがき
1章 アルゴリズムで考える
1.1 問題を理解する
1.2 素朴解
1.3 賢い方式
1.3.1 貪欲法
1.3.2 分割統治法
1.3.3 並列法
1.3.4 近似法
1.3.5 一般化
1.4 まとめ
1.5 参考文献
2章 アルゴリズムの数学
2.1 問題インスタンスのサイズ
2.2 関数の成長率
2.3 最良、平均、最悪時の分析
2.3.1 最悪時
2.3.2 平均時
2.3.3 最良時
2.3.4 下限と上限
2.4 性能分類
2.4.1 定数的振る舞い
2.4.2 対数的振る舞い
2.4.3 d<1に対する下位線形 O(nd)の振る舞い
2.4.4 線形性能
2.4.5 線形対数(nlog n)の性能
2.4.6 二乗の性能
2.4.7 あまり明白でない性能を示す計算
2.4.8 指数性能
2.4.9 漸近的成長のまとめ
2.5 ベンチマーク演算
2.6 参考文献
3章 アルゴリズムの構成要素
3.1 アルゴリズムテンプレートの形式
3.2 疑似コードのテンプレート形式
3.3 評価実験の形式
3.4 浮動小数点計算
3.4.1 性能
3.4.2 丸め誤差
3.4.3 浮動小数点数値の比較
3.4.4 特殊な値
3.5 アルゴリズム例
3.5.1 名前と概要
3.5.2 入出力
3.5.3 文脈
3.5.4 解
3.5.5 分析
3.6 一般的なアプローチ
3.6.1 貪欲法
3.6.2 分割統治
3.6.3 動的計画法
3.7 参考文献
4章 整列アルゴリズム
4.0.1 用語
4.0.2 表現
4.0.3 比較可能な要素
4.0.4 安定整列
4.0.5 整列アルゴリズムの選択基準
4.1 転置ソート
4.1.1 挿入ソート
4.1.2 文脈
4.1.3 解
4.1.4 分析
4.2 選択ソート
4.3 ヒープソート
4.3.1 文脈
4.3.2 解
4.3.3 分析
4.3.4 変形
4.4 分割ベースのソート
4.4.1 文脈
4.4.2 解
4.4.3 分析
4.4.4 変形
4.5 比較なしの整列
4.6 バケツソート
4.6.1 解
4.6.2 分析
4.6.3 変形
4.7 外部ストレージのある整列
4.7.1 マージソート
4.7.2 入出力
4.7.3 解
4.7.4 分析
4.7.5 変形
4.8 整列ベンチマーク結果
4.9 分析技法
4.10 参考文献
5章 探索
5.1 逐次探索
5.1.1 入出力
5.1.2 文脈
5.1.3 解
5.1.4 分析
5.2 二分探索
5.2.1 入出力
5.2.2 文脈
5.2.3 解
5.2.4 分析
5.2.5 変形
5.3 ハッシュに基づいた探索
5.3.1 入出力
5.3.2 文脈
5.3.3 解
5.3.4 分析
5.3.5 変形
5.4 ブルームフィルタ
5.4.1 入出力
5.4.2 文脈
5.4.3 解
5.4.4 分析
5.5 二分探索木
5.5.1 入出力
5.5.2 文脈
5.5.3 解
5.5.4 分析
5.5.5 変形
5.6 参考文献
6章 グラフアルゴリズム
6.1 グラフ
6.1.1 データ構造の設計
6.2 深さ優先探索
6.2.1 入出力
6.2.2 文脈
6.2.3 解
6.2.4 分析
6.2.5 変形
6.3 幅優先探索
6.3.1 入出力
6.3.2 文脈
6.3.3 解
6.3.4 分析
6.4 単一始点最短経路
6.4.1 入出力
6.4.2 解
6.4.3 分析
6.5 密グラフ用ダイクストラ法
6.5.1 変形
6.6 単一始点最短経路選択肢の比較
6.6.1 ベンチマークデータ
6.6.2 密グラフ
6.6.3 疎グラフ
6.7 全対最短経路
6.7.1 入出力
6.7.2 解
6.7.3 分析
6.8 最小被覆木アルゴリズム
6.8.1 入出力
6.8.2 解
6.8.3 分析
6.8.4 変形
6.9 グラフについての考察
6.9.1 ストレージの問題
6.9.2 グラフ分析
6.10 参考文献
7章 AIにおける経路探索
7.1 ゲーム木
7.1.1 静的評価関数
7.2 経路探索の概念
7.2.1 状態の表現
7.2.2 可能な手の計算
7.2.3 拡張深さの限度
7.3 ミニマックス
7.3.1 入出力
7.3.2 文脈
7.3.3 解
7.3.4 分析
7.4 ネグマックス
7.4.1 解
7.4.2 分析
7.5 アルファベータ法
7.5.1 解
7.5.2 分析
7.6 探索木
7.6.1 経路長のヒューリスティック関数
7.7 深さ優先探索
7.7.1 入出力
7.7.2 文脈
7.7.3 解
7.7.4 分析
7.8 幅優先探索
7.8.1 入出力
7.8.2 文脈
7.8.3 解
7.8.4 分析
7.9 A*探索
7.9.1 入出力
7.9.2 文脈
7.9.3 解
7.9.4 分析
7.9.5 変形
7.10 探索木アルゴリズムの比較
7.11 参考文献
8章 ネットワークフローアルゴリズム
8.1 ネットワークフロー
8.2 最大フロー
8.2.1 入出力
8.2.2 解
8.2.3 分析
8.2.4 最適化
8.2.5 関連アルゴリズム
8.3 二部マッチング
8.3.1 入出力
8.3.2 解
8.3.3 分析
8.4 増加道についての考察
8.5 最小コストフロー
8.6 積み替え
8.6.1 解
8.7 輸送
8.7.1 解
8.8 割り当て
8.8.1 解
8.9 線形計画法
8.10 参考文献
9章 計算幾何学
9.1 問題の分類
9.1.1 入力データ
9.1.2 計算
9.1.3 タスクの性質
9.1.4 仮定
9.2 凸包
9.3 凸包走査
9.3.1 入出力
9.3.2 文脈
9.3.3 解
9.3.4 分析
9.3.5 変形
9.4 線分交差を計算する
9.5 線分走査法
9.5.1 入出力
9.5.2 文脈
9.5.3 解
9.5.4 分析
9.5.5 変形
9.6 ボロノイ図
9.6.1 入出力
9.6.2 解
9.6.3 分析
9.7 参考文献
10章 空間木構造
10.1 最近傍クエリ
10.2 範囲クエリ
10.3 交差クエリ
10.4 空間木構造
10.4.2 四分木
10.5 最近傍法
10.5.1 入出力
10.5.2 文脈
10.5.3 解
10.5.4 分析
10.5.5 変形
10.6 範囲クエリ
10.6.1 入出力
10.6.2 文脈
10.6.3 解
10.6.4 分析
10.7 四分木
10.7.1 入出力
10.7.2 解
10.7.3 分析
10.7.4 変形
10.8.1 入出力
10.8.2 文脈
10.8.3 解
10.8.4 分析
10.9 参考文献
11章 新たな分類のアルゴリズム
11.1 方式の種類
11.2 近似アルゴリズム
11.2.1 入出力
11.2.2 文脈
11.2.3 解
11.2.4 分析
11.3 並列アルゴリズム
11.4 確率的アルゴリズム
11.4.1 集合のサイズを推定する
11.4.2 探索木のサイズを推定する
11.5 参考文献
12章 結び:アルゴリズムの諸原則
12.1 汝のデータを知れ
12.2 問題を小さく分割せよ
12.3 正しいデータ構造を選べ
12.4 空間と時間のトレードオフを使え
12.5 探索を構築せよ
12.6 問題を別の問題に帰着させよ
12.7 アルゴリズムを書くのは難しい、アルゴリズムをテストするのはさらに難しい
12.8 可能なら近似解を受け入れよ
12.9 性能を上げるために並列性を加えよ
付録A ベンチマーク
A.1 統計の基礎
A.2 例
A.2.1 Javaベンチマーク
A.2.2 Linuxベンチマーク
A.2.3 Pythonベンチマーク
A.3 報告
A.4 精度
訳者あとがき
索引






