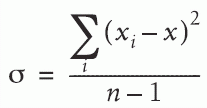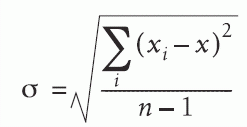| 位置 | 誤 | 正 |
pxi
下から
12行目 |
http://www.oreilly.co.jp/books/9780596514286/(日本語) |
http://www.oreilly.co.jp/books/9784873114286/(日本語) |
p26
下から
8行目 |
while (hight - low <= 2){
|
while (hight - low >= 2){
(原書正誤表に従い修正) |
p27
2段落
3行目 |
その導関数をf'(x)=x*cos(x)+sin(x)-5-sin(x)=x*cos(x)-5とする。
|
その導関数をf'(x)=x*cos(x)+sin(x)-5+sin(x)=x*cos(x)+2*sin(x)-5とする。
(原書正誤表に従い修正) |
p27
表2-2 |
■ |

(原書正誤表に従い修正) |
p39
表2-6 |
■ |
(原書正誤表に従い修正) |
p65
††訳注 |
文字""は「文字がない」符号と考えることも可能で |
文字"¬"は「文字がない」符号と考えることも可能で |
p77
5行目 |
図4-10の各行は、ループの中で、軸値(この場合は要素「06」)。以下の
|
図4-10の各行は、ループの中で、軸値(この場合は要素「06」)以下の
|
p88
図4-12
上部 |
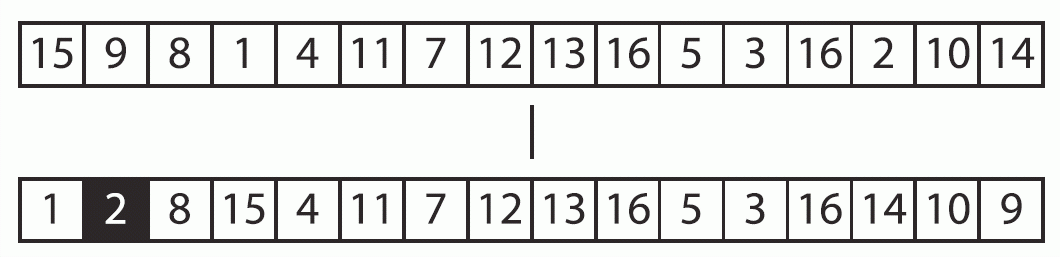
■ |
(原書正誤表に従い修正) |
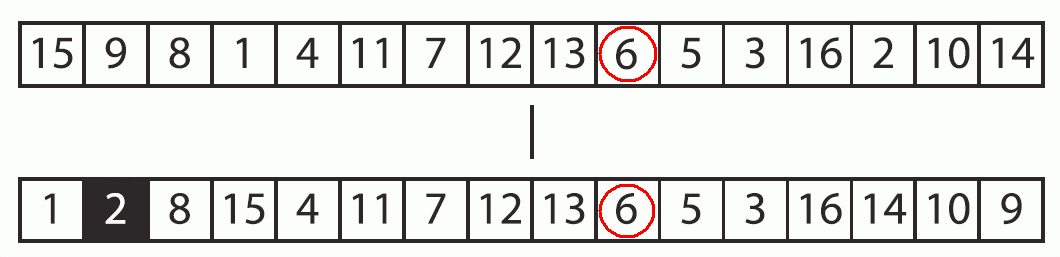
p89
図4-13
上部 |

■ |

(原書正誤表に従い修正) |
p92
4.4.5.2
1行目 |
例4-3の分割法では、 |
例4-3の関数partitionでは、 |
p92
4.4.5.2
3行目 |
再帰段階での部分配列のサイズが変動するかもしれない。最初の部分配列と2番目の部分配列との間で、軸値に等しい要素を入れ替えれば釣り合いが取れる。 |
再帰段階での部分配列のサイズが偏るかもしれない。軸値に等しい要素は、最初の部分配列と2番目の部分配列に交互に入れれば釣り合いが取れる。 |
p96
図4-14
9. |
swap A[i]
|
swap A[idx]
(原書正誤表に従い修正) |
p123
5.3.1
1行目 |
二分探索の入力は、添え字付きの集まりAである。
|
二分探索の入力は、整列済みの添え字付きの集まりAである。
(原書正誤表に従い修正) |
p128
図5-3 |
1. 与えられたサイズの配列
2. for i = 0 to n - 1 do
3. h = hash(C[i])
4. if A[h]が空である then
5. A[h] = new Linked List
6. add C[i] to A[h]
7. return A |
1. A = 与えられたsizeの配列
2. for i = 0 to n - 1 do
3. h = hash(C[i])
4. if A[h]が空である then
5. A[h] = new Linked List
6. C[i]をA[h]に追加する
7. return A |
p141
12行目 |
再ハッシュ機能を利用できる。 |
再ハッシュ機能を導入できる。 |
p154
4行目 |
経路<v3, v1, v5, v4, v2, v1, v5, v4, v2 >は閉路となるが、これは
|
経路<v3, v1, v5, v4, v2, v1, v5, v4, v2 >には閉路が含まれるが、それは
|
p154
最終行 |
new int[4096][4096]で2次元配列を作ろうとすると
|
new int[8192][8192]で2次元配列を作ろうとすると
(原書正誤表に従い修正) |
p160
図6-9
1. |
foreachv ∈ V do
|
foreach v ∈ V do
(原書正誤表に従い修正) |
p186
例6-8
コメント
1行目 |
sからtへの経路を節点のベクトルとして
|
sからtへの経路を節点のリストとして
(原書正誤表に従い修正) |
p211
下から
2行目 |
図の中で濃い灰色の20個の盤面状態は、 |
図の中で薄い灰色の20個の盤面状態は、
(原書正誤表に従い修正) |
p212
下から
5行目 |
例7-3に示す実装では、 |
例7-4に示す実装では、 |
p221
表7-3 |
BadEvaluatorのh*(n)の記述
空の升目は無視する。 |
真ん中と空の升目は無視する。
(原書正誤表に従い修正) |
p238
1行目 |
×が対角線でゲームを勝つことができる、負けてしまう盤面も調べていた。
|
×が対角線でゲームを勝つことができる、○が負けてしまう盤面も調べていた。
|
p247
下から
2行目 |
ネットワーク全体の容量が十分あるとして、
|
ネットワーク全体の容量を満たすだけの十分な量の商品を流せるとして、
|
p250
下から
3行目 |
非負のフローと容量を保証するので、
|
非負のフローと容量の下で、
|
p276
下から
2行目 |
IPointと交差するか、IRectangleを含むか判定できる。 |
IPointまたはIRectangleを含むか判定できる。 |
p277
図9-1
IRectangle
5行目 |
+boolean intersects(IPoint) |
+boolean contains(IPoint) |
p277
図9-1
ILineSegment
9行目 |
IPoint intersection(ILineSegment) |
IPoint intersection(ILineSegment)†
†訳注:intersectionは、交差がなければnullを返すが、あれば、その点を返す。 |
p278
3行目 |
境界値が固定次元の[left, right]であるn次元立方体を表し、 |
各次元での境界値が[left, right]であるn次元立方体を表し、 |
p288
6行目 |
点集合が大きくなくても処理できる。 |
点集合が大きくても処理できる。 |
p291
9.2.7
2段落
2行目 |
実は明示的に整列配列をする必要はない。 |
実は明示的に配列を整列する必要はない。 |
p292
図9-12 |
平行二分木 |
平衡二分木
(3箇所) |
p292
3行目 |
2種類のデータ分布と |
3種類のデータ分布と
(原書正誤表に従い修正) |
p295
図9-14
左側 |
プロセスS1
(図)
プロセスS2
(図)
プロセスS3
(図)
プロセスS4
|
S1を処理
(図)
S2を処理
(図)
S3を処理
(図)
S4を処理
|
p308
9.4.3
3行目 |
①葉の節点が木の同じレベルにあり、 |
①葉の節点が木の同じレベルにあるか、 |
p309
下から
8行目 |
標準選択演算に負けてしまう。 |
標準的な選択演算に負けてしまう。 |
p313
下から
9行目 |
ただし、最近接質問点は、単位正方形内のままにする。 |
ただし、最近傍質問点は、単位正方形内のままにする。 |
p316
9.4.7
1行目 |
根から親へと節点をさかのぼって走査する。 |
根から親へと節点を戻って走査する。 |
p316
図9-24
中央の3. |
3. foreach descendant d of node do |
3. foreach ノードの子孫節点d do |
p345
表11-4
タイトル |
表11-4 7章のAIでの経路発見 |
表11-4 7章のAIでの経路発見アルゴリズム |
p347
表11-6
直前 |
表11-6は、9章で取り上げた計算幾何学をまとめる。 |
表11-6は、9章で取り上げた計算幾何学アルゴリズムをまとめる。 |
p347
表11-6
タイトル |
表11-6 9章の計算幾何学 |
表11-6 9章の計算幾何学アルゴリズム |
p352
7行目 |
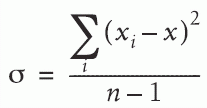 |
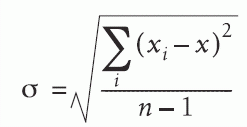
(原書正誤表に従い修正) |
p359
A.3.3
2行目 |
1章で使ったこの例では、 |
2章例2-7で使ったこの例では、
(原書正誤表に従い修正) |
p362
5行目 |
例A-8の関数largeAddは、n個の数の集まりをまとめて加算する。 |
例A-8の関数largeAddは、n個の数の集まりをまとめて加算する†。
†訳注:原著者によると、このコードでは次のScheme実装に依存した書き方をしている。必ずしも標準規格に沿ってはいない点に注意。
MzScheme version 207, Copyright (c) 2004 PLT Scheme, Inc. |
p365
下から
12行目 |
プラットフォーム間で実行時間を比較したい時もある。
|
プラットフォーム間で実行時間を比較したい時に使えない。
|
p365
下から
9行目 |
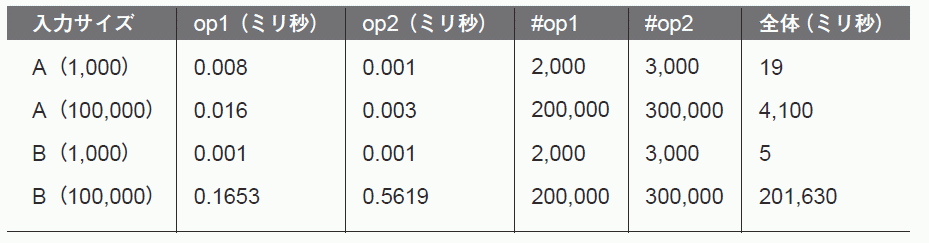
表A-3のデータを見直すと、
|
表A-4のデータを見直すと、
|
![[cover photo]](https://www.oreilly.co.jp/books/images/picture_large978-4-87311-428-6.jpeg)