近年のゲーム開発では3DCGや物理シミュレーションなどの技術が多用されているため、その基盤である数学についての理解なしに商業ベースのゲーム開発はありえません。本書では、ゲーム開発や3DCGで用いらる数学的な要素――デカルト座標系、ベクトル、行列、線型代数、オイラー角、四元数、座標変換(平行移動、回転、拡大縮小)、幾何形状プリミティブの種類と構造体、プリミティブの可視性と衝突判定といった3D数学、さらにはグラフィックス用の3D数学――についてサンプルを多用しながらわかりやすく解説します。
原書(英語版)のWebページ
●原著者によるサポートサイト
実例で学ぶゲーム3D数学
Fletcher Dunn, Ian Parberry 著、松田 晃一 訳
![[cover photo]](https://www.oreilly.co.jp/books/images/picture_large978-4-87311-377-7.jpeg)
- TOPICS
- Programming , Game , Math
- 発行年月日
- 2008年10月
- PRINT LENGTH
- 484
- ISBN
- 978-4-87311-377-7
- 原書
- 3D Math Primer for Graphics and Game Development
- FORMAT
関連ファイル
正誤表
ここで紹介する正誤表には、書籍発行後に気づいた誤植や更新された情報を掲載しています。以下のリストに記載の年月は、正誤表を作成し、増刷書籍を印刷した月です。お手持ちの書籍では、すでに修正が施されている場合がありますので、書籍最終ページの奥付でお手持ちの書籍の刷版、刷り年月日をご確認の上、ご利用ください。
正誤表 - 2008年11月掲載(2刷以降は修正済み)
■P.vii 下から4行目
- 【誤】本書は入門書であり、普通は数ページでさっとごまかされたり、他の本では付録に追いやられていたりする話題である、基本的な3Dの概念をカバーすることに力を注いでいます(結局のところ、みなさんはこの手の内容はすでにすべて知っているためです)。
- 【正】本書は入門書であり、普通は数ページでさっとごまかされたり、他の本では付録に追いやられていたりする話題(結局のところ、みなさんはこの手の内容はすでにすべて知っているためです)である、基本的な3Dの概念をカバーすることに力を注いでいます。
- 【誤】閉め切り
- 【正】締め切り
- 【誤】問に
- 【正】問いに
- 【誤】「1」、「2」などの数
- 【正】「1」、「2」などの数字
- 【誤】礼儀正しい
- 【正】洗練された
- 【誤】今問題になっているように、
- 【正】今のところそうだとされているように、
- 【誤】それ以来私たちは、数えるべきものがなくなってしまったのです
- 【正】それ以来私たちは、数えるべきものがなくなってしまうのです
- 【誤】電話、殺菌剤
- 【正】電話機の除菌剤
- 【誤】数え尽くしてしまったのです
- 【正】数え尽くしてしまうのです
- 【誤】その結果、自然数の有限な(確かに大きいですが、有限な)部分集合だけを用いる必要がありますが、私たちは宇宙を離散数学だけで記述できるということになります。
- 【正】その結果、私たちは宇宙を離散数学だけで記述できるということになります。自然数の有限な(確かに大きいですが、有限な)部分集合を用いるだけでいいのです。
- 【誤】みなさんが実世界で
- 【正】みなさんは実世界で
- 【誤】記述されます。
- 【正】説明できます。
- 【誤】人間が探検するのに数分かかるような
- 【正】人間が探検するのに数分以上かかるような
- 【誤】適度の広さの仮想現実
- 【正】適当な種類の仮想現実
- 【誤】なのでしょか?
- 【正】なのでしょうか?
- 【誤】+zがページの内側を指して
- 【正】+zがページの奥を指して
- 【誤】+zがページの外側を向いて
- 【正】+zがページの手前を向いて
- 【誤】勉強しましょう。
- 【正】よく見てください。
- 【誤】仮想世界が存続
- 【正】仮想世界が存在
- 【誤】ローカルな子空間ではなく
- 【正】ローカルな子座標空間ではなく
- 【誤】回転によって慣性空間とワールド空間
- 【正】回転によってオブジェクト空間と慣性空間
- 【誤】基準座標系の文脈で
- 【正】基準座標系の中で
- 【誤】点とベクトルの間の関数は
- 【正】点とベクトルの間の混乱は
- 【誤】任意の点に対して相対的でない量を扱う場合が多いのです。
- 【正】任意の点に対して[_Fb_]相対的でない量[_/Fb_]を扱う場合が多いのです。
- 【誤】線型代数の教科書で一般化されてしまっていると
- 【正】線型代数の教科書が行っているくらいに一般化されたレベルでは、
- 【誤】集合について
- 【正】任意の集合について
- 【誤】式4-17 内積を使って2つのベクトルのなす角を計算する
- 【正】式4-17 内積を使って2つのベクトルのなす角を計算する†
- 【誤】式4-18 2つの単位ベクトルのなす角を計算する†
- 【正】式4-18 2つの単位ベクトルのなす角を計算する
- 【誤】2Dベクトルにだけ適用されます。
- 【正】3Dベクトルにだけ適用されます。
- 【誤】内積
- 【正】外積
- 【誤】a・(b×c)は定義されません。
- 【正】(a・b)×cは定義されません。
- 【誤】||a||^2 + ||b||^2 = ||a + b||^2 ベクトルの足し算に適用したピタゴラスの定理。
- 【正】||a||^2 + ||b||^2 = ||a + b||^2 ベクトルの足し算に適用したピタゴラスの定理。ただしaとbは原点からのベクトルで直交している。
- 【誤】よいクラスの設定は
- 【正】よいクラスの設計は
- 【誤】これらは、インターネット上のコードをみたり、自分で試してみてあまりよい考えでないことがわかったりします
- 【正】これらは、インターネット上に置かれているコードで見かけたりしますが、自分で試してみるとあまりよい考えでないことがわかります。
- 【誤】オーバーロードされた演算子は、外積用の関数呼び出しよりもエレガントなものにはならないのです。しかしながら、このオーバーロードされた演算子は、関数呼び出しよりも、明らかにわかりやすくはないのです。%と×の類似がわからないプログラマは特にそうです。
- 【正】しかしながら、このオーバーロードされた演算子は、関数呼び出しよりも、明らかにわかりやすくはないのです。%と×の類似がわからないプログラマは特にそうですが、オーバーロードされた演算子は、外積用の関数呼び出しよりもエレガントなものにはならないのです。
- 【誤】ベクトル表現
- 【正】ベクトル式
- 【誤】ベクトル表現
- 【正】ベクトル式
- 【誤】// しかし、ベクトル表現を持つ場合は、非メンバ関数スタイルは不格好に見える
- 【正】// しかし、ベクトル式を持つ場合は、メンバ関数スタイルは不格好に見える
- 【誤】ベクトル表現
- 【正】ベクトル式
- 【誤】また、アクセス関数の使用も
- 【正】また、アクセス関数の使用は
- 【誤】(点と線の間には明確な線引きが存)在することが多いのです
- 【正】(点と線の間には明確な線引きが存)在しないことが多いのです
- 【誤】ベクトル表現
- 【正】ベクトル式
- 【誤】ベクトル表現
- 【正】ベクトル式
- 【誤】どんな線型変換でも
- 【正】どのような線型変換でも
- 【誤】解釈されることが説明しています。
- 【正】解釈されることを説明しました。
- 【誤】また箱や補助物体を使うとまた想像し
- 【正】また箱や補助物体を使うと想像し
- 【誤】この図全体(座標空間および車)を、座標空間をページの標準方向に戻すように回転させてみます
- 【正】この座標空間がこのページの「標準」方向に戻るように、この図全体(座標空間と車)を回転させてみます
- 【誤】均等スケーリングの実行になります
- 【正】均等スケーリングになります
- 【誤】面積と体積は
- 【正】面積や体積は
- 【誤】代数による見方からは
- 【正】代数的な観点からは
- 【誤】の形をした任意の変換はアフィン変換です
- 【正】の形をした変換はすべてアフィン変換です
- 【誤】余因子は
- 【正】余因子(cofactor)は
- 【誤】影響を与えないが、
- 【正】影響を与えずに、
- 【誤】符号付き面積です
- 【正】符号付き体積です
- 【誤】行列が負なら、
- 【正】行列式が負なら、
- 【誤】もしくはその両方
- 【正】もしくはその片方
- 【誤】そういった場合です
- 【正】このケースです
- 【誤】ベクトルの自身との
- 【正】あるベクトルと自分自身との
- 【誤】それぞれ直交
- 【正】お互いに直交
- 【誤】ために直交基底が必要
- 【正】ために正規直交基底が必要
- 【誤】1つのパスで
- 【正】1回の処理で
- 【誤】すべての点について
- 【正】すべての点については
- 【誤】これと同じ基本的考え方を
- 【正】これと基本的に同じ考え方を
- 【誤】7章では、3×3の行列を多くの基本的な座標変換のために紹介しました。
- 【正】7章では、多くの基本的な座標変換用の3×3行列を示しました。
- 【誤】投影の中心
- 【正】投影の中心(ピンホール)
- 【誤】反対向き
- 【正】逆向き
- 【誤】行列の座標変換の実際の向き
- 【正】実際の行列の座標変換の向き
- 【誤】6つの制限が満たされる必要があります。
- 【正】満たされるべき6つの制約があります。
- 【誤】6つの制限
- 【正】6つの制約
- 【誤】最小のデータ量
- 【正】最少のデータ量
- 【誤】ωを否定する
- 【正】ωの符号を反転する
- 【誤】私たちにとって
- 【正】四元数は私たちにとって
- 【誤】設定されています
- 【正】設計されています
- 【誤】// 完全なasin関数を用いる必要はない
- 【正】// 安全なasin関数を用いる必要はない
- 【誤】剛体の座標変換
- 【正】剛体変換
- 【誤】tz = 1.0f;
- 【正】tz = 0.0f;
- 【誤】剛体の座標変換
- 【正】剛体変換
- 【誤】剛体でない座標変換
- 【正】非剛体変換
- 【正】バウンディグボックス
- 【誤】バウンディングボックス
- 【誤】バンディング
- 【正】バウンディング
- 【誤】テキストマップ
- 【正】テクスチャマップ
- 【誤】「おまけ」な
- 【正】「おまけ」の
- 【誤】数が数えらるとすると、
- 【正】数が数えられるとすると、
- 【誤】void raytrace(Vector3 rayOrg, Vector3 rayDelta, float &minT);
- 【正】void rayTrace(Vector3 rayOrg, Vector3 rayDelta, float &minT);
- 【誤】void Node::raytrace(Vector3 rayOrg, Vector3 rayDelta, float &minT) {
- 【正】void Node::rayTrace(Vector3 rayOrg, Vector3 rayDelta, float &minT) {
- 【誤】objPtr->rayTrace(rayOrg, rayDelta);
- 【正】objPtr->rayTrace(rayOrg, rayDelta, minT);
- 【誤】=φである
- 【正】=φである。
正誤表 - 2010年6月掲載(5刷以降は修正済み)
■P.164 式9-9
- 【誤】
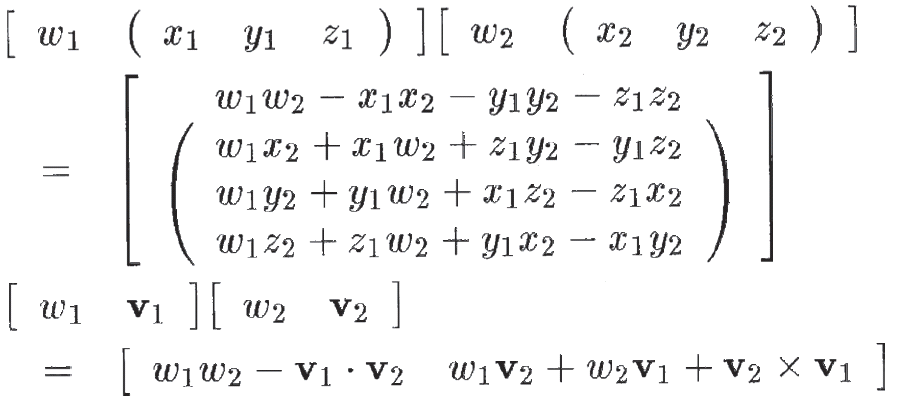
- 【正】
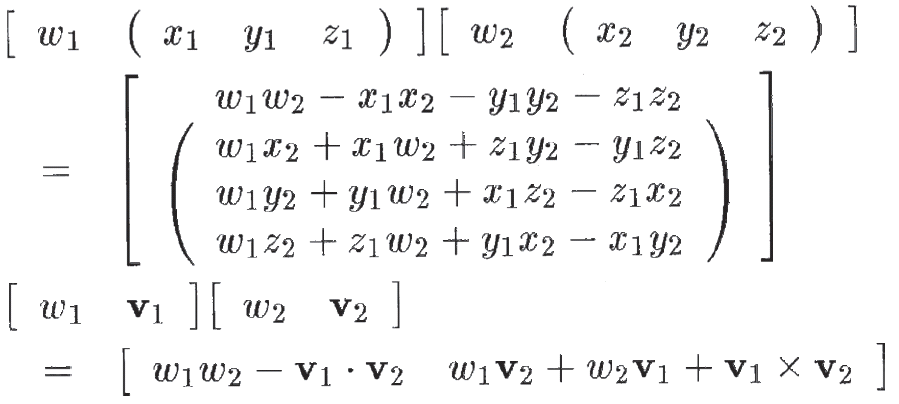
- 【誤】
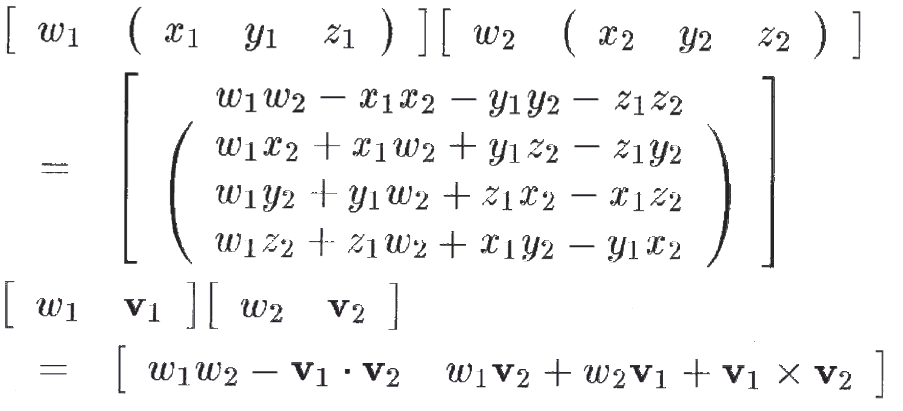
- 【正】
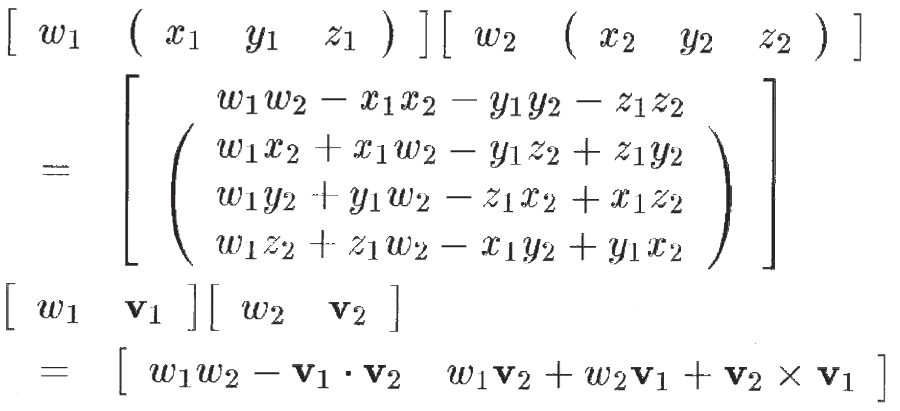
- 【誤】m13 = xx*q.z - ww*q.x
- 【正】m13 = xx*q.z - ww*q.y
目次
訳者まえがき まえがき 1章 デカルト座標系 1.1 1D数学 1.2 2Dデカルト数学 1.2.1 例:架空の町デカルト 1.2.2 任意の2D座標空間 1.2.3 デカルト座標を用いて2Dで場所を指定する 1.3 2Dから3Dへ 1.3.1 もう1つの次元、もう1つの軸 1.3.2 3Dで位置を指定する 1.3.3 左手座標系と右手座標系 1.3.4 本書で使われる重要な慣習 1.4 練習問題 2章 複数の座標空間 2.1 なぜ複数の座標空間を使うのか? 2.2 便利な座標空間 2.2.1 ワールド空間 2.2.2 オブジェクト空間 2.2.3 カメラ空間 2.2.4 慣性空間 2.3 入れ子になった座標空間 2.4 座標空間を指定する 2.5 座標空間の変換 2.6 練習問題 3章 ベクトル 3.1 ベクトル ─ 数学的な定義 3.1.1 ベクトルとスカラー 3.1.2 ベクトルの次元 3.1.3 記法 3.2 ベクトル ─ 幾何学的な定義 3.2.1 ベクトルはどのように見えるか? 3.2.2 位置と移動 3.2.3 ベクトルを指定する 3.2.4 一連の移動としてのベクトル 3.3 ベクトルと点 3.3.1 相対位置 3.3.2 点とベクトルの関係 3.4 練習問題 4章 ベクトルの演算 4.1 線型代数 vs. 私たちが必要とするもの 4.2 フォントの約束事 4.3 ゼロベクトル 4.4 ベクトルの反転 4.4.1 線型代数の公式 4.4.2 幾何学的解釈 4.5 ベクトルの大きさ(長さ) 4.5.1 線型代数の公式 4.5.2 幾何学的解釈 4.6 ベクトルにスカラーを掛ける 4.6.1 線型代数の公式 4.6.2 幾何学的解釈 4.7 ベクトルの正規化 4.7.1 線型代数の公式 4.7.2 幾何学的解釈 4.8 ベクトルの足し算と引き算 4.8.1 線型代数の公式 4.8.2 幾何学的解釈 4.8.3 ある点から別の点へのベクトル 4.9 距離の公式 4.10 ベクトルの内積 4.10.1 線型代数の公式 4.10.2 幾何学的解釈 4.10.3 あるベクトルを別のベクトルへ投影する 4.11 ベクトルの外積 4.11.1 線型代数の公式 4.11.2 幾何学的解釈 4.12 線型代数の恒等式 4.13 練習問題 5章 簡単な3Dベクトルクラス 5.1 クラスのインタフェース 5.2 Vector3クラスの定義 5.3 設計上の決定 5.3.1 単精度浮動小数点と倍精度浮動小数点 5.3.2 演算子オーバーロード 5.3.3 最も重要な演算だけを提供する 5.3.4 よけいな演算子をオーバーロードしない 5.3.5 定数型メンバ関数を用いる 5.3.6 const&引数を用いる 5.3.7 メンバ関数と非メンバ関数 5.3.8 デフォルトの初期化処理なし 5.3.9 仮想関数を使用しない 5.3.10 情報隠蔽を使わない 5.3.11 グローバルなゼロベクトル定数 5.3.12 Point3クラスはない 5.3.13 最適化に関して 6章 行列入門 6.1 行列 ─ 数学的な定義 6.1.1 行列の次元と表記法 6.1.2 正方行列 6.1.3 行列としてのベクトル 6.1.4 転置 6.1.5 行列にスカラーを掛ける 6.1.6 2つの行列の掛け算 6.1.7 ベクトルと行列を掛ける 6.1.8 行ベクトルと列ベクトル 6.2 行列 ─ 幾何学的解釈 6.2.1 どうやって行列はベクトルを座標変換するのでしょうか? 6.2.2 行列はどのように見えるでしょう? 6.2.3 まとめ 6.3 練習問題 7章 行列と線型変換 7.1 オブジェクトの変換と座標空間の変換 7.2 回転 7.2.1 2Dにおける回転 7.2.2 基本軸の周りの3D回転 7.2.3 任意の軸の周りの3D回転 7.3 スケーリング 7.3.1 基本軸に沿ったスケーリング 7.3.2 任意の向きでのスケーリング 7.4 正投影 7.4.1 基本軸または基本平面への投影 7.4.2 任意の直線や平面上への投影 7.5 リフレクション 7.6 せん断 7.7 座標変換の合成 7.8 座標変換の分類 7.8.1 線型変換(一次変換) 7.8.2 アフィン変換 7.8.3 可逆変換 7.8.4 角度保存変換 7.8.5 直交変換 7.8.6 剛体変換 7.8.7 座標変換のタイプのまとめ 7.9 練習問題 8章 より詳しい行列の説明 8.1 行列式 8.1.1 線型代数の公式 8.1.2 幾何学的解釈 8.2 逆行列 8.2.1 線型代数の公式 8.2.2 幾何学的解釈 8.3 直交行列 8.3.1 線型代数の公式 8.3.2 幾何学的解釈 8.3.3 行列の直交化 8.4 4×4の同次座標行列 8.4.1 4D同次空間 8.4.2 4×4の平行移動行列 8.4.3 一般的なアフィン変換 8.4.4 透視投影 8.4.5 ピンホールカメラ 8.4.6 4×4の行列を使った透視投影 8.5 練習問題 9章 3Dにおける方向と角変位 9.1 方向とは何か? 9.2 行列形式 9.2.1 どの行列? 9.2.2 行列形式の長所 9.2.3 行列形式の短所 9.2.4 まとめ 9.3 オイラー角 9.3.1 オイラー角とは何か? 9.3.2 その他のオイラー角の約束事 9.3.3 オイラー角の長所 9.3.4 オイラー角の短所 9.3.5 まとめ 9.4 四元数 9.4.1 四元数の表記法 9.4.2 複素数としての四元数 9.4.3 軸と角度の対としての四元数 9.4.4 四元数の符号反転 9.4.5 恒等四元数 9.4.6 四元数の大きさ 9.4.7 四元数の共役と逆数 9.4.8 四元数の乗算(外積) 9.4.9 四元数の差分 9.4.10 四元数の内積 9.4.11 四元数の対数(log)、指数(exp)、スカラーによる乗算 9.4.12 四元数の累乗 9.4.13 四元数の補間 ─ 別名“slerp” 9.4.14 四元数のスプライン ─ 別名“squad” 9.4.15 四元数の長所と短所 9.5 手法の比較 9.6 表現間の変換 9.6.1 オイラー角から行列への変換 9.6.2 行列からオイラー角への変換 9.6.3 四元数から行列への変換 9.6.4 行列から四元数への変換 9.6.5 オイラー角から四元数への変換 9.6.6 四元数からオイラー角への変換 9.7 練習問題 10章 C++による座標変換 10.1 概説 10.2 EulerAnglesクラス 10.3 Quaternionクラス 10.4 RotationMatrixクラス 10.5 Matrix4x3クラス 11章 幾何形状プリミティブ 11.1 表現手法 11.1.1 陰関数形式 11.1.2 パラメトリック形式 11.1.3 直接形式 11.1.4 自由度 11.2 直線と光線 11.2.1 2点による表現 11.2.2 パラメトリックな光線の表現 11.2.3 直線の特別な2D表現 11.2.4 表現間の変換 11.3 球と円 11.4 バウンディングボックス 11.4.1 AABBの表現 11.4.2 AABBの計算 11.4.3 AABB vs. バウンディングスフィア 11.4.4 AABBの座標変換 11.5 平面 11.5.1 陰関数形式 ─ 平面の方程式 11.5.2 3点を使った定義 11.5.3 4つ以上の点に対する最適合平面 11.5.4 点から平面への距離 11.6 三角形 11.6.1 三角形の基本的性質 11.6.2 三角形の面積 11.6.3 重心空間 11.6.4 特別な点 11.7 ポリゴン 11.7.1 単純ポリゴンvs.複合ポリゴン 11.7.2 自己交差ポリゴン 11.7.3 凸ポリゴン vs. 凹ポリゴン 11.7.4 三角形分割と扇状の分割 11.8 練習問題 12章 幾何テスト 12.1 2Dの陰関数形式の直線上の最も近い点 12.2 パラメトリックな光線上の最も近い点 12.3 平面上の最も近い点 12.4 円/球上の最も近い点 12.5 AABBで最も近い点 12.6 交差テスト 12.7 2Dの陰関数形式の2本の直線の交差 12.8 3Dにおける2本の光線の交差 12.9 光線と平面の交差 12.10 AABBと平面の交差 12.11 3つの平面の交差 12.12 光線と円/球との交差 12.13 2つの円/球の交差 12.14 球とAABBの交差 12.15 球と平面の交差 12.16 光線と三角形の交差 12.17 光線とAABBの交差 12.18 2つのAABBの交差 12.19 他のテスト 12.20 AABB3クラス 12.21 練習問題 13章 三角形メッシュ 13.1 メッシュを表現する 13.1.1 インデックス付き三角形メッシュ 13.1.2 高度なテクニック 13.1.3 レンダリングに特化した表現 13.1.4 頂点キャッシュ 13.1.5 三角形ストリップ 13.1.6 三角形ファン 13.2 付加的なメッシュ情報 13.2.1 テクスチャマップ座標 13.2.2 面の法線 13.2.3 ライティングの値 13.3 トポロジーと一貫性 13.4 三角形メッシュの操作 13.4.1 区分操作 13.4.2 頂点を1つに貼り合わせる 13.4.3 面を分離する 13.4.4 辺の破壊 13.4.5 メッシュの破壊 13.5 C++の三角形メッシュクラス 14章 グラフィックス用の3D数学 14.1 グラフィックスパイプラインの概要 14.2 視野のパラメータを設定する 14.2.1 出力ウィンドウを指定する 14.2.2 ピクセルの縦横比 14.2.3 視錐台 14.2.4 視野とズーム 14.3 座標空間 14.3.1 モデリング空間とワールド空間 14.3.2 カメラ空間 14.3.3 クリップ空間 14.3.4 スクリーン空間 14.4 ライティングとフォグ 14.4.1 色に関する数学 14.4.2 光源 14.4.3 標準のライティングの方程式 ─ 概要 14.4.4 鏡面成分 14.4.5 拡散成分 14.4.6 環境成分 14.4.7 光の減衰 14.4.8 ライティングの方程式 ─ すべてを一緒にする 14.4.9 フォグ 14.4.10 フラットシェーディングとグーローシェーディング 14.5 バッファ 14.6 テクスチャマップ処理 14.7 幾何形状の生成と送出 14.7.1 LODの選択とプロシージャルモデリング 14.7.2 APIへの幾何形状の送出 14.8 座標変換とライティング 14.8.1 クリップ空間への座標変換 14.8.2 頂点のライティング 14.9 裏面カリングとクリッピング 14.9.1 裏面カリング 14.9.2 クリッピング 14.10 ラスタライズ処理 15章 可視性の決定 15.1 バウンディグボリュームテスト 15.1.1 視錐台に対するテスト 15.1.2 オクルージョンをテストする 15.2 空間分割テクニック 15.3 グリッド方式 15.4 四分木と八分木 15.5 BSPツリー 15.5.1 古典的なBSP 15.5.2 任意の分割面 15.6 オクルージョンカリングテクニック 15.6.1 潜在的な可視集合 15.6.2 ポータルテクニック 付録A 数学の復習 A.1 総和の記号 A.2 角度、度、ラジアン A.3 三角関数 A.4 三角恒等式 付録B ゲーム開発者のための確率・統計入門 B.1 確率 B.1.1 確率の基礎 B.1.2 集合 B.1.3 確率と集合 B.1.4 統計的確率 B.1.5 条件付き確率 B.2 統計 B.2.1 度数分布 B.2.2 資料の代表値 B.2.3 資料のちらばり B.2.4 確率変数と確率分布 B.2.5 さまざまな分布 B.3 乱数 B.3.1 疑似乱数 B.3.2 疑似乱数の性能評価 B.3.3 メルセンツイスタ B.4 さいごに 付録C 参考文献 あとがき 索引

